Algorithmen vs. Mensch: Über die Schwierigkeiten im Umgang mit Vorurteilen und statistischen Wahrscheinlichkeiten

Eine Kolumne von Frank Preßler

In der aktuellen Diskussion positionieren sich viele Menschen an den Enden der möglichen Meinungsskala: Algorithmen sind entweder furchtbar und angsteinflößend oder aber der Heilsbringer. Die Wahrheit, sofern es überhaupt eine gibt, dürfte irgendwo dazwischenliegen. Die aktuelle Kolumne soll nur einen winzigen Ausschnitt beleuchten: Die Feststellung von Wahrscheinlichkeiten bei relativ einfachen Fragestellungen. Am Ende werden Sie sehen: Es ist alles viel komplexer als erwartet.

Im ersten Schritt soll nur kurz auf das Problem vorurteilsbehafteter Entscheidungen eingegangen werden. Befürworter algorithmischer Systeme sagen, dass diese in der Lage seien, im Gegensatz zu Menschen vorurteilsfreie Entscheidungen treffen zu können. Nicht nur deshalb sind solche Systeme auch bereits in einigen amerikanischen Staaten im Justizbereich im Einsatz. In Österreich nutzt der dortige Arbeitsmarktservice AMS seit Ende 2018 Algorithmen zur Bewertung, ob sich Investitionen in Maßnahmen für Arbeitssuchende lohnen. Das Problem: Statistische Ist-Daten werden losgelöst vom Individuum zum Bewertungsmaßstab. Das Ergebnis: Wer weiblich und über 50 ist, wird praktisch algorithmisch aussortiert, weil es sich nicht mehr lohnt. Die Reaktionen auf die AMS-Algorithmen waren dementsprechend negativ.

Selbst wenn also die Algorithmen gut und bewusst vorurteilsfrei programmiert sind, was an sich schon eine Herausforderung birgt, bleibt wie zuvor skizziert ein weiteres Problem: die Datenbasis. Hierzu ein weiteres Beispiel: Mitte 2016 hat das Nachrichtenportal ProPublica umfangreich über einen Algorithmus namens COMPAS berichtet, der Zukunftsprognosen über Straftäter in Florida erstellt[1]. Das Ergebnis: Bei Angeklagten, die nach der Freilassung nicht wieder straffällig wurden, war die prognostizierte Rückfallwahrscheinlichkeit bei Schwarzen doppelt so hoch wie bei Weißen. Genau umgekehrt war es bei den Angeklagten, die erneut straffällig wurden: Hier wurden doppelt so viel Weiße als geringes Risiko eingestuft wie Schwarze. Warum was das so, wo doch der Algorithmus nachweislich die Hautfarbe nicht betrachtete?

Nun, im Kern handelt es sich um ein mathematisches Problem, das nicht auflösbar ist und zumindest in Teilen nur deshalb auftritt, weil die bisherige Rechtsprechung besonders in Amerika nachweislich vorurteilsbehaftet war. Mit anderen Worten: Der Algorithmus kann so gut sein wie möglich, die Ergebnisse sind gleichwohl von Vorteilen geprägt. Es gilt die alte Weisheit im Algorithmen-Umfeld: SISO[2]! Und damit zum Kern des Themas:

Sehr viele Entscheidungsfehler, egal ob durch Maschinen oder Menschen, entstehen durch mangelhafte Kenntnisse über statistische Effekte. Oftmals versagt hierbei die Intuition, wenn Wahrscheinlichkeiten für bestimmte Ereignisse zu schätzen sind. Der britische Mathematiker und Philosoph Tomas Bayes (1701 bis 1761) hat in diesem Bereich maßgebliche Arbeit in der Wahrscheinlichkeitsrechnung geleistet, die bis heute allgemein gültig ist. Mangelhafte Kenntnis hierüber führen auch heute täglich zu falschen Entscheidungen, Stereotypen und Vorurteilen. Die heutige mITgedacht-Kolumne will hierzu einen bescheidenen Beitrag der Aufklärung und Erläuterung leisten und hierzu einige Beispiele anführen, die helfen sollen, das Problem zu verstehen.

1. Das Taxi-Problem
Als eines der bekanntesten Beispiele für die verzerrenden Effekte der Statistik gilt das Taxi-Problem[3], das wie folgt definiert ist:

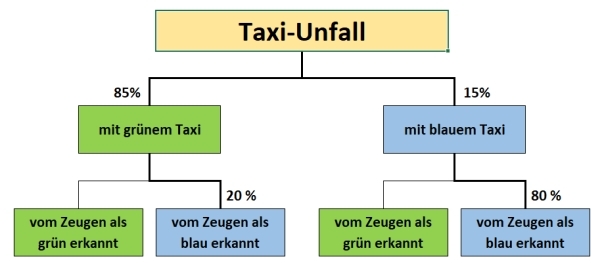
- In einer Stadt existieren zwei Taxi-Unternehmen: „Green Cab” mit grünen Taxis und „Blue Cab” mit blauen Taxis. Der Marktanteil von „Green Cab” liegt bei 85%, womit 15% Marktanteil für „Blue Cab” verbleiben.

- Es kommt zu einem Verkehrsunfall mit Fahrerflucht und einem einzigen Zeugen. Dieser Zeuge gibt an, der Fahrer eines blauen Taxis habe den Unfall verursacht.

- Das Gericht überprüft die Zuverlässigkeit des Zeugen unter den Umständen des Unfalls (Nacht, dunkel) und gelangt zu dem Schluss, dass der Zeuge in 80% aller Fälle die Farbe richtig erkennt. Frage: Wie hoch ist die Wahrscheinlichkeit, dass das an dem Unfall beteiligte Taxi der Firma „Blue Cab“ gehörte?

Wie fällt Ihre Antwort aus? 80%? Es wäre durchaus normal, denn in den intuitiven Antworten wird üblicherweise der Wert benannt, der auch schon in der Fallbeschreibung steht, also die besagten 80% der richtigen Erkennung durch den Zeugen. Jedoch wird bei dieser Antwort die als Basisrate bezeichnete Grundlage ausgeklammert, die die Marktanteile der Taxis konkret beziffert. Eine erste Idee von der richtigen Antwort erhält man, wenn das Problem grafisch dargestellt wird.

Ähnlich wie schon zuvor lässt sich die Lösung einfach visualisieren:

Hier wird die Basisrate (85% zu 15%) in eine Beziehung mit der Wahrscheinlichkeit einer richtigen Zuordnung durch den Zeugen (80% zu 20%) gesetzt. In der Formel nach Bayes wird die Wahrscheinlichkeit des zu untersuchenden Ereignisses (blaues Taxi wird als blau erkannt) in das Verhältnis zur Summe der bedingten Wahrscheinlichkeiten aller Ereignisketten gesetzt (blaues Taxi wird als blau erkannt und grünes Taxi wird als blau erkannt)[4]. Die Antwort lautet dann: 41%.

Es ist erkennbar, dass die Verzahnung von statistischen Basisraten mit davon vermeintlich losgelösten Ereignissen dazu führen, dass oftmals die statistischen Daten nicht ausreichend berücksichtigt werden. Wenn wie hier am Beispiel gesehen lediglich 15% aller Taxis blau sind, dann muss schon aus logischen Gesichtspunkten der falschen Zeugenwahrnehmung (20%) eine wesentlich höhere Bedeutung zukommen als intuitiv erwartbar war.

2. Sensivität und Spezifität
Ein ganz wesentlicher Einfluss dieser Erkenntnis existiert auch im medizinischen Kontext bei der Fragestellung, inwieweit beispielsweise Testverfahren zu richtigen oder falschen Ergebnissen führen. In diesem Themenkomplex hat der deutsche Psychologe Gerd Gigerenzer über viele Jahre regelrechte Aufklärungsarbeit leisten müssen, um Risiken von Erkrankungen oder Testverfahren aber auch Heilungschancen objektiv richtig zu bewerten. Ganz wesentliche Standards der Risiko-Darstellung gehen auf Gigerenzers Arbeiten zurück[5].

Bei Testverfahren zur Erkennung von Krankheiten werden stets die Begriffe der Sensitivität und Spezifität angegeben. Die Sensitivität zeigt die Wahrscheinlichkeit eines positiven Ergebnisses bei bestehender Erkrankung an, die Spezifität die Wahrscheinlichkeit eines negativen Ergebnisses bei keiner vorliegenden Erkrankung[6]. Von entscheidender Bedeutung und stetige Ursache von Fehlentscheidungen ist der Gegenpol der Spezifität: die sogenannte Falsch-Positiv-Rate. Auch hierzu ein erstes Beispiel[7] zur Veranschaulichung:

Ein Tourist befürchtet, von einer seltenen Krankheit angesteckt worden zu sein. Der Test liefert zu 99% ein positives Ergebnis, wenn die Krankheit vorhanden ist. Die Spezifität, also das korrekte, negative Ergebnis bei Nichtvorliegen der Krankheit, liegt bei 98%. Bekannt ist auch, dass sich durchschnittlich nur jeder tausendste Tourist ansteckt. Der Tourist hat ein positives Untersuchungsergebnis bekommen. Wie hoch ist die Wahrscheinlichkeit, dass er sich tatsächlich angesteckt hat?

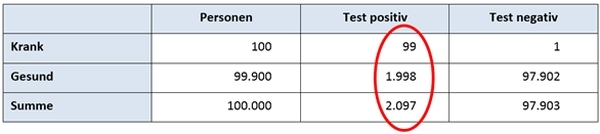
Ähnlich wie schon zuvor lässt sich die Lösung einfach visualisieren:

Die Wahrscheinlichkeit ergibt sich aus der Relation der richtigen Positiv-Ergebnisse zur Gesamtzahl aller Positiv-Ergebnisse, also: 99/2097 = 4,7%.

Trotz der hohen Erkennungsrate von 99% bei einer vorliegenden Erkrankung ist es also nur zu weniger als 5% wahrscheinlich, dass ein positives Ergebnis auch richtig ist. Hätten Sie das erwartet? Es ist wenig verwunderlich, dass auch Experten, also in diesem Fall ganz besonders Ärzte, nicht in der Lage sind, auf Basis der vorliegenden, objektiven Datensätze korrekte Wahrscheinlichkeiten zu berechnen. Die Auswirkungen auf die Qualität von Beratungsgesprächen sind insofern schnell erkennbar, ebenso auf die daraus resultierenden Entscheidungen. Probieren Sie es aus: Sollten Sie einmal, egal in welchem Kontext, einen medizinischen Test machen, fragen Sie vorher nach der Wahrscheinlichkeit, mit der ein positives Testergebnis aussagt, dass auch wirklich eine Erkrankung oder ein bestimmter Blutwert usw. vorliegt. Fragen Sie danach, es gilt immerhin der Grundsatz des informierten Patienten bzw. der informierten Einwilligung[8].

3. Die Überwachung am Berliner Bahnhof Südkreuz
Die Bedeutung dieses Themas der bedingten Wahrscheinlichkeiten und den statistischen Grundlagen nach Bayes geht weit über die Medizin hinaus und ist auch immer wieder eine erheblich vernachlässigte Größe in tagesaktuellen Themen wie derzeit der automatisierten Personen- und auch Automobil-Überwachungssysteme. Die mITgedacht-Kolumne will nicht gesellschaftspolitische Entscheidungen kommentieren und bewerten, der Anspruch besteht vielmehr darin, einen Erkenntnisgewinn zu vermitteln und zum Mitdenken anzuregen. So auch hier:

Anfang August 2017 startete die Bundespolizei das Projekt „Biometrische Gesichtserkennung“ und beendete dieses ein Jahr später am 31.07.2018. Das Projekt hatte eine hohe mediale Aufmerksamkeit und wurde kritisch in Bezug auf Themen der staatlichen Überwachung verfolgt. Dem Abschlussbericht zufolge liegt die Sensitivitätsrate bei 80%, die Falsch-Positiv-Rate zwischen 0,12% und 0,67%[9]. Die Ergebnisse wurden seitens der Bundespolizei sehr positiv bewertet, gleichwohl stellt sich die Frage, ob diese Sichtweise gerechtfertigt ist.

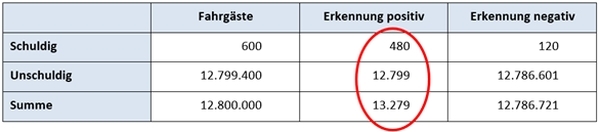
Lassen Sie uns hierzu faktenbasierte Daten sammeln: Die Deutsche Bahn befördert nach eigenen Angaben 12,8 Millionen Fahrgäste pro Tag in Bahnen und Bussen[10]. Sie alle passieren typischerweise Bahnhöfe unterschiedlichster Größe. Unter der Annahme eines flächendeckenden Aufbaus der biometrischen Gesichtserkennung als langfristiges Ziel ist die Zahl der täglichen Fahrgäste mithin die statistische Basisrate. Die polizeiliche Eigenbewertung geht davon aus, dass sich Fahndungserfolge insbesondere im Kontext islamistischer Gefährder*innen erzielen lassen würden, deren Zahl sich auf rund 600 beläuft[11]. Welche Ergebnisse würden also bei einer flächendeckenden Überwachung erzielt werden? Die folgende Darstellung geht bereits zu Gunsten des polizeilichen Abschlussberichts von einer Falsch-Positiv-Rate von nur 0,1% aus.

Die tatsächliche Trefferquote läge bei 480/13.279 = 3,6% und es würden täglich tausende von Bahnreisenden unschuldig verdächtigt werden. Auch wenn die Anzahl der Gesuchten deutlich steigen würde, indem jede Art von gesuchtem Straftäter erfasst würde, bliebe die Falsch-Positiv-Quote nominal erheblich hoch.

Dieses Praxisbeispiel zeigt deutlich, wie wichtig die Betrachtung der Falsch-Positiv-Quote ist. Im konkreten Fallbeispiel sind 0,1% offensichtlich keine gute Quote, diese müsste vielmehr erheblich geringer sein.

4. Die Überwachung von Flugpassagieren
Das letzte und aktuellste Beispiel ist nicht minder interessant: Wie die Süddeutsche Zeitung am 24.04.2019 berichtete[12], erfasst das BKA seit Ende 2018 die Daten aller Flugpassagiere, die in Deutschland starten oder landen, um diese mit Fahndungslisten abzugleichen. Der software-getriebene Abgleich sorgte in Zahlen ausgedrückt für 94.098 sogenannte „technische Treffer“ im Zeitraum August 2018 bis März 2019 bei rund 1,2 Millionen Passagieren. Unter diesem Begriff wird lediglich verstanden, dass der automatisierte Abgleich zwischen Passagierdaten und der BKA-Fahndungsdatei zu einem Treffer führte. Diese 94.098 Treffer wurden sodann manuell geprüft. Nach dieser fachlichen Prüfung blieben übrig: 277. Das ergibt eine Falsch-Positiv-Rate von 99,7%. Bei einer solchen Quote ist die Rate der richtigen Erkennungen quasi irrelevant und das System schlicht unbrauchbar.

5. Fazit
Das Denken in Wahrscheinlichkeiten und prozentualen Quoten ist oftmals abstrakt und nur schwer greifbar. Schon bei der Frage, was eigentlich eine Regenwahrscheinlichkeit von 30% im Wetterbericht bedeutet, kennen viele Menschen nicht die richtige Antwort. Da viele Entscheidungen auf Basis von Zahlen erfolgen, sind Zweifel stets angebracht, wenn derartige Quoten und Raten genutzt werden sollen. Schon die Nutzung von absoluten Zahlen statt Prozentwerten hilft weiter. So finden Sie beispielsweise in vielen Risikoaufklärungen im medizinischen Bereich längst Angaben wie „1 von 100.000“ statt 0,001%, da diese Art der Darstellung für die allermeisten Menschen deutlich verständlicher ist. Der „Satz von Bayes“ als sein wichtigstes Werk wurde vor 255 Jahren publiziert und ist zweifelsfrei Standard in Schulen und Universitäten, soweit es um Statistik geht. Die Relevanz ist hoch und wird es dank der Allgemeingültigkeit auch bleiben.

Und um den Kreis zum Anfang zu schließen: Menschen treffen keine besseren Entscheidungen als Maschinen. Wir sind nicht nur genauso sondern deutlich stärker anfällig für Vorurteile und Bewertungsfehler, und auch wir können mathematische Grundlagen nicht ändern. Wenn aktuelle Systeme lediglich auf Basis von historischen Ist-Daten arbeiten, so werden frühere, diskriminierende und menschengemachte Entscheidungen in die Zukunft in Form von maschinengemachten Entscheidungen fortgeschrieben. Das kann nicht das Ziel sein. Es muss parallel zum Ist-Stand einen Soll-Stand geben, der tatsächlich diskriminierungsfreie Ergebnisse vorsieht. Der Weg ist dann das Ziel: der sukzessive Übergang und die Überwindung aller Varianten von Vorurteilen.

Eine künftige Lösung wird daher in der Symbiose von Maschinen und Menschen liegen, indem beide ihre Stärken ausspielen: Maschinen können Daten vorsortieren und Muster entdecken, besser als alle Menschen. Ein abschließendes Urteil muss jedoch immer einem Menschen obliegen, da uns ansonsten auch das verloren geht, was uns selbst ausmacht: das Menschsein als solches.